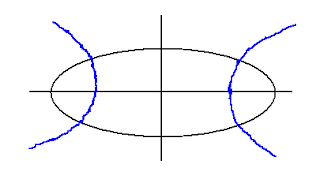
A family of ellipse whose one member is shown in the figure is not expected to be self-orthogonal. But, when the equation $\frac{1}{{{x^2} + \lambda }} + \frac{1}{{{y^2} + \lambda }} = 1$ is analysed using differential equation technique, one finds that the equation does represent self-orthogonal trajectory. How does one visualise this type of trajectory?
The answer lies in the possible values of $ \lambda $ which is a parameter or arbitrary constant. The expression $\frac{1}{{{x^2} + \lambda }} + \frac{1}{{{y^2} + \lambda }}$ can become negative for several negative values of $ \lambda $ and hence the curve can become hyperbola. Now, one can visualise self-orthogonality in the following manner:
It can be seen that the curves above intersect at 90 degrees.